Ji Shaoyou (1963- ) is a native of Puning, Guangdong province. He graduated from a major of geophysical structure, Ocean Geology Department, Shandong Marine College (currently known as Ocean University of China) in 1984 and received a master's degree of the same major from the same university in 1987. He is now working for China National Offshore Oil Nanhai East Corporation as an engineer. During his postgraduate time, he was mainly engaged in study of scalar wave equation turning-wave finite difference method and related software development. After graduation, he took up study of method of data handling for geophysics and software development. In 1986-1987, he joined an aid project of United Nations Development Programme (NUDP) called "Oil Geophysics Prospecting Data Processing Software Development". His major achievement in this project was his new method of wave equation migration--Accurate wave equation migration and developed a practical manufacturing module--FULWM in the computer CYBER730 of Beijing Computer Center, Ministry of Geology. In 1987-1988, he developed seismic data migration processing software ---FWEMIG for production in the computer VAX of China National Offshore Oil Nanhai East Corporation. He published over 10 academic theses.
DEVELOPMENT OF SEISMIC MIGRATION THEORY AND PRACTICE
Ma Zaitian
(Tongji University, Shanghai)
Abstract
None of the large and middle oii fields in the world has been discovered without using the technique of seismic prospecting after the World War II The main work of studying the subsurface structures is the seismic migration processing with large computer. The modern seismic migration technique was pioneered by J.F. Claerbout at the Stanford University in the 1970s.His equation adapts to only single geological structure with dip angles 0o -- 15o.
To break out the dip limitation of Claerbout's equation we put forward a new theory, method and technique, which are playing an important role in the completion of modern seismic imaging technique. The idea and method described here have been popularized in China and abroad.
For the best imaging seismic observation data we worked out a new higher-order partial differential equation and its solution. The solution was obtained by using our 'order-splitting' method. The higher-order partial differential equation used in seismic migration was derived as follows:
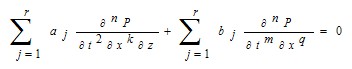(1)
where n is the order number of the equation; i=1, 2, 3？？？, r[r=(n+1)/2),if n is odd; r=n/2, if n is even]; =n-1, n-2, n-3, ？？？ , r; k=0,2,4, ？？？ , r; j=1, 2, 3, ？？？ , s (s=n-r); m =1, 3, 5, ？？？ , if n is odd; m=0, 2, 4, ？？？ , if n is even ; q=2,4,6, ？？？.
The equation (1) is a new type of partial differential equation; it cannot be solved by conventional method. We proposed a new scheme called order-splitting method to solve it. In numerical mathematics, the dimension-splitting method has been used, but the order-splitting method is not existed before. By the order-splitting method the high-order equation (1) can be transformed into a system of second-order partial differential equations:
(2)
j=1,2,3, ？？？ , n-1.
Each equation in (2) is a parabolic-type equation. We have proved that it is well- posed and stable in computation. The system of equations (2) is equivalent to the original equation (1).
The method was tested by theoretical and practical seismic data, and the results show that the order-splitting method is excellent in seismic migration. The research has scientific and practical useful value. It has been playing an important role in the study of complex geological subsurface structures for exploration and production of oil and gas in every region where they exist.